11-1 동적 계획법이란?
동적 계획법도 분할 정복과 같이 문제를 더 작은 부분으로 나눈 후 답을 계산하여 답들로부터 원래 문제의 해답을 구하는 구조
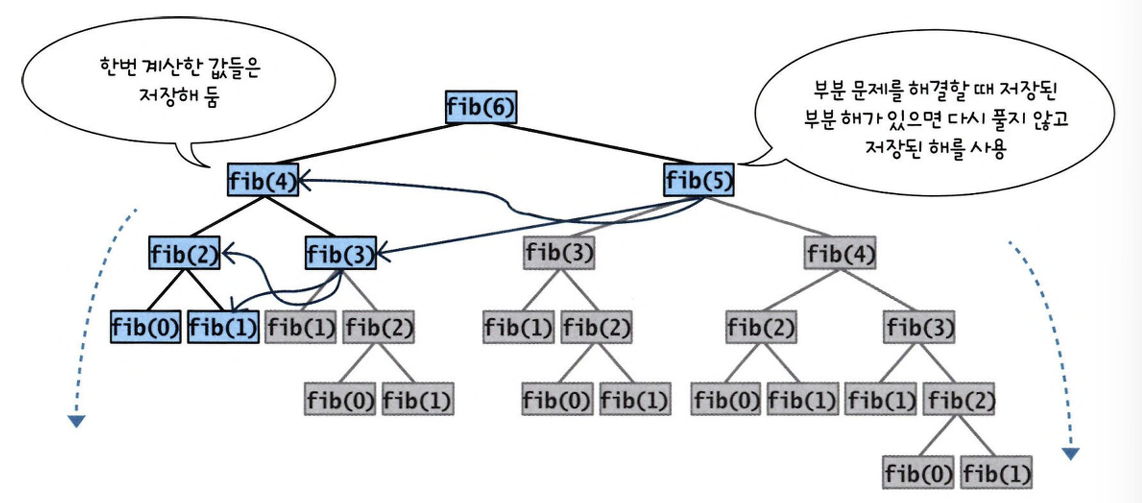
동적 계획법은 부분 문제들의 답을 어딘가에 저장해 둔 뒤 필요할 때 다시 꺼내서 사용하는 전략을 사용한다는 점에서 차이 존재
피보나치 수열 문제

n번째 피보나치 수를 구하는 fib(n)은 위와 같이 순환 관계로 나타낼 수 있음
순환 관계는 분할 정복을 이용하여 해결할 수 있으나, 심각한 계산 중복 문제가 발생하고, 시간 복잡도가 O(2^n)
동적 계획법은 구한 답을 저장하여 재사용 → 다시 풀어야 할 때는 저장된 해답을 이용
부분 문제의 해를 저장하는 방법에는 메모이제이션과 테이블화가 있음
메모이제이션을 이용한 피보나치 수열
메모이제이션(memoization): 함수의 결과를 저장할 때 메모리를 미리 준비해서 계산한 값을 저장해 두었다가 재활용하는 방법
하향식(top-down)으로 문제 해결
피보나치 수열(메모이제이션 이용)
def fib_dp_mem(n):
if (mem[n]==None):
if n<2:
mem[n]=n
else:
mem[n]=fib_dp_mem(n-1)+fib_dp_mem(n-2)
return mem[n]전역변수 mem은 크기가 n+1인 리스트로, mem[k]에는 k번째 피보나치 수가 저장됨
모든 부분 문제가 한 번씩 처리됨, 부분 문제의 수: n
⇒ O(n)의 시간 복잡도
테이블 mem의 용량은 n에 비례
⇒ O(n)의 공간 복잡도
테이블화를 이용한 피보나치 수열
테이블화(tabulation, 타뷸레이션)는 부분 문제의 해를 메모리에 저장할 때, 테이블 항목들을 순서대로 채워나감
상향식(bottom-up)으로 문제 해결
- 결과를 저장할 테이블(table) 준비, fib(n)을 구하려면 크기가 n+1인 테이블 필요
- 기반 상황의 답을 테이블에 채움
이미 알고 있는 fib(0), fib(1)의 답을 먼저 테이블에 저장한 후 가장 작은 부분 문제부터 순서대로 해를 구해 테이블을 채워서 올라감 - 원래의 문제 fib(n)을 구할 때까지 진행
피보나치 수열(테이블화 이용)
def fib_dp_tab(n):
f = [None] + (n+1)
f[0] = 0
f[1] = 1
for i in range(2, n+1):
f[i] = f[i-1] + f[i-2]
return f[n]시간 복잡도: O(n), 공간 복잡도: O(n)
동적 계획법을 이용한 문제 해결 전략
- 분할 정복 전략 적용 가능해야 함
- 중복된 문제를 반복해서 해결하는 경우여야 함
- 최적 부분 구조 특성이 있어야 함 → 부분 문제의 최적해를 이용하여 전체 문제를 해결할 수 있는 구조
위의 조건들을 만족하면 동적 계획법을 적용할 수 있음
메모제이션과 테이블화 중 하나를 선택하여 구현
11-2 최장 공통 부분 순서
최장 공통 부분 순서(LCS: Longest Common Subsequence)
부분 순서(subsequence): 어떤 시퀀스의 일부분으로 상대적인 순서를 유지하는 것
LCS 문제: 두 데이터에 공통으로 들어 있는 부분 순서 중에서 가장 긴 것을 찾는 문제
LCS 길이의 순환 관계식
길이가 각각 m과 n인 두 문자열 X=<x1, x2, ..., xm>, Y=<y1, y2, ..., yn>가 주어졌을 때, LCS 길이 l(Xm, Yn)을 구하는 문제
기반 상황
n이나 m이 0이라면 공통 문자가 없으므로 LCS의 길이는 0
l(X0, Yn)과 l(Xm, Y0) 모두 0
일반 상황
n과 m이 모두 0이 아닌 경우, X와 Y의 맨 뒤의 문자부터 같은 경우와 다른 경우로 분리하여 처리
- (Case 1) X와 Y의 마지막 문자가 같은 경우(xm = yn): 해당 문자를 X와 Y에서 모두 빼고 LCS 길이를 구한 다음 1을 더함
마지막 문자를 빼고 구한 LCS의 길이: l(Xm-1, Yn-1)
⇒ 전체 LCS 길이: l(Xm-1, Yn-1) + 1 - (Case 2) X와 Y의 마지막 문자가 다른 경우(xm ≠ yn): 두 가지 시도 가능
1) X에서 마지막 문자를 빼고 Y와 비교(l(Xm-1, Yn))
2) Y에서 하나를 빼고 X와의 LCS 구함(l(Xm, Yn-1))
1)과 2) 중 큰 값이 최종 결과 → l(Xm, Yn) = max(l(Xm-1, Yn), l(Xm, Yn-1))

순환구조의 알고리즘
LCS의 길이(분할 정복)
def lcs_recur(X, Y, m, n):
if m==0 or n==0:
return 0
elif X[m-1]==Y[n-1]:
return 1 + lcs_recur(X, Y, m-1, n-1)
else:
return max(lcs_recur(X, Y, m, n-1), lcs_recur(X, Y, m-1, n))
동적 계획버(테이블화)에 의한 LCS 길이
테이블 준비
부분 해를 저장할 테이블 이름을 L이라 하면, L의 크기: (m+1) × (n+1)
m=0이나 n=0인 기반 상황은 이미 답을 알고 있으므로 L[0][n] = L[m][0] = 0 으로 모두 초기화

LCS 길이 알고리즘
def lcs_dp(X, Y):
m = len(X)
n = len(Y)
L = [[None]*(n+1) for _ in range(m+1)]
for i in range(m+1):
for j in range(n+1):
if i==0 or j==0:
L[i][j] = 0
elif X[i-1] == Y[j-1]:
L[i][j] = L[i-1][j-1] + 1
else:
L[i][j] = max(L[i-1][j], L[i][j-1])
return L[m][n]
LCS 추적 알고리즘
LCS의 길이뿐만 아니라 두 문자열의 LCS 자체를 구하려는 경우, 앞에서 구한 테이블을 이용하여 LCS를 구할 수 있음
- LCS의 요소들을 담기 위한 리스트 준비
- 오른쪽 아래의 요소가 현재 셀에 해당
- 현재 셀의 값이 ←, ↖, ↑ 방향으로 인접한 셀들의 값보다 모두 크면 현재 셀의 값을 리스트의 전단에 삽입, 현재 셀의 위치를 ↖로 한 칸 이동
- 3의 조건이 만족하지 않는 경우, 현제 셀의 값이 ← 셀과 같고, ↑ 셀보다 크면 현재 셀을 왼쪽으로 옮김
- 3과 4의 조건이 모두 만족하지 않으면 현재 셀을 위쪽으로 옮김
- 3~5 과정을 i나 j가 0이 될 때까지 반복
LCS 테이블에서 LCS를 추적하는 알고리즘
def lcs_dp_traceback(X, Y, L):
lcs = ""
i = len(X)
j = len(Y)
while i > 0 and j > 0:
v = L[i][j]
if v > L[i][j-1] and v > L[i-1][j] and v > L[i-1][j-1]:
i -= 1
j -= 1
lcs = X[i] + lcs
elif v == L[i][j-1] and v > L[i-1][j]: j -= 1
else: i -= 1
return lcs
11-3 배낭 채우기
무게와 가치가 각각 주어진 n개의 물걸을 용량이 W인 배낭에 넣을 때, 배낭의 가치가 최대가 되도록 하는 문제
배낭 문제의 순환 관계식
0-1 배낭 문제에서 주어진 문제와 부분 문제 사이의 관계를 순환 관계로 구함
용량이 W인 배낭과 n개의 물건 E1, E2, ..., En이 주어지는데, 각 물건은 Ei = (wgt i, val i)와 같이 무게 wgt i 와 가치 val i를 가짐
배낭의 가치: A(k, w) → k개의 물건 E1~Ek를 용량이 w인 배낭에 넣는 경우의 배낭의 최대가치
기반상황
배낭에 넣을 물건이 없는 경우(k=0) 배낭 용량과 상관없이 최대가치=0 → A(0, w) = 0
배낭의 용량이 0인 경우(w=0) 배낭의 최대가치=0 → A(k, 0) = 0
일반상황
k개의 물건 E1~Ek을 용량이 w인 배낭에 넣을 때의 최대가치 A(k, w)
Case 1: k번째 물건의 무게 wgt k 가 남은 배낭 용량 w보다 크면(wgt k > w), 해당 물건은 배낭에 넣을 수 없음
→ 최대가치는 E1~Ek-1만으로 계산 (A(k, w) = A(k-1, w))
Case 2: Ek를 배낭에 넣을 수 있다면(wgt k =< w), Ek를 넣는 경우와 그렇지 않은 경우의 최대가치를 구해야 함
- Ek를 배낭에 넣는 경우: 배낭의 최대가치는 val k만큼 증가, 배낭의 용량은 w-wgt k
용량이 w-wgt k인 배낭에 E1~Ek-1를 넣는 문제 해결 A(k-1, wgt k)
최대가치 = val k + A(k-1, w-wgt k) - Ek를 배낭에 넣지 않는 경우: 배낭의 최대가치나 용량은 변하지 않고 고려해야 할 물건이 하나 감소
Ek를 제외한 나머지를 용량 w의 배낭에 넣을 때의 최대가치를 구하면 됨 A(k-1, w)

분할 정복 알고리즘
0-1 배낭 채우기(분할 정복)
def knapSack_dc(W, wt, val, n):
if n == 0 or W == 0:
return 0
if (wt[n-1] > W):
return knapSack_dc(W, wt, val, n-1)
else:
valWithout = knapSack_dc(W, wt, val, n-1)
valWith = val[n-1] + knapSack_dc(W-wt[n-1], wt, val, n-1)
return max(valWith, valWithout)
동적 계획법에 의한 0-1 배낭 문제 해법
동적 계획법을 적용하기 위해서는 물건의 무게와 배낭의 용량을 모두 정수로 제한하는 조건을 추가해야 함
테이블 설계
최대가치가 물건의 개수 n과 배낭의 용량 W의 함수 A(n, w)로 표시되므로 변수 두 개
→ (n+1) × (W+1)의 2차원 배열 형태

기반 상황
A(0, W)=0, A(n, 0)=0 → n=0인 행, W=0인 열 모두 0으로 채움
일반 상황
A(i, w) 셀 계산 위해서 A(i-1, w-wt i), A(i-1, w) 사용, A(i, w)의 위쪽이나 왼쪽에 계산되어 있음
최종적인 해답은 표의 맨 오른쪽 아래 셀에 저장
배낭 채우기 알고리즘
배낭 채우기(동적 계획법)
def kanpSack_dp(W, wt, val, n):
A = [[0 for x in range(W + 1)] for x in range(n+1)]
for i in range(1, n+1):
for w in range(1, W+1):
if wt[i-1] > w:
A[i][w] = A[i-1][w]
else:
valWith = val[i-1] + A[i-1][w-wt[i-1]]
valWithout = A[i-1][w]
A[i][w] = max(valWith, valWithout)
return A[n][W]
복잡도 분석
테이블의 모든 칸을 채우기 위해 이중 루프 사용
채워야 할 칸(일반 상황)의 수: n × W
⇒ 시간 복잡도: O(nW), 공간 복잡도: O(nW)
'ECC - 알고리즘 > 자료구조와 알고리즘 with 파이썬' 카테고리의 다른 글
| Chapter12. 공간으로 시간벌기와 백트래킹 (0) | 2025.06.24 |
|---|---|
| Chapter09. 억지 기법과 탐욕적 전략 (0) | 2025.05.20 |
| Chapter08. 그래프 (0) | 2025.05.16 |
| Chapter07. 탐색 (0) | 2025.05.08 |
| Chapter06. 정렬 (0) | 2025.05.03 |